Paso del modelo E-R al modelo relacional  

Existen varias reglas para convertir cada uno de los elementos de los diagramas E-R en tablas:

1. Para cada conjunto de entidades fuertes se crea una relación con una columna para cada atributo.
2. Para cada conjunto de entidades débiles se crea una relación que contiene una columna para los atributos que forman la clave primaria de la entidad fuerte a la que se encuentra subordinada y una columna para cada atributo de la entidad.
3. Para cada interrelación se crea una relación que contiene una columna para cada atributo correspondiente a las claves principales de las entidades interrelacionadas.
4. Lo mismo para entidades compuestas, añadiendo las columnas necesarias para los atributos añadidos a la interrelación.

Las relaciones se representan mediante sus esquemas, la sintaxis es simple:

<nombre_relación>(<nombre_atributo_i>,...)

La clave principal se suele indicar mediante un subrayado.

Veamos un ejemplo, partamos del siguiente diagrama E-R:

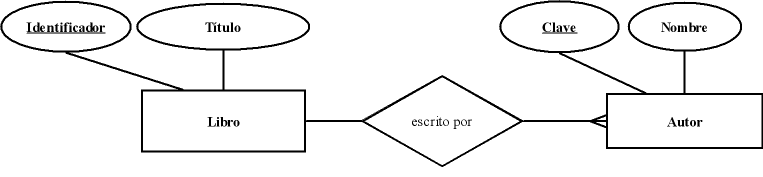
Siguiendo las normas indicadas obtendremos las siguientes relaciones:

Libro(Identificador, Título)
Autor(Clave, Nombre)
Escrito_por(Identificador, Clave)

Manipulación de datos, álgebra relacional  

El modelo relacional también define el modo en que se pueden manipular las relaciones. Hay que tener en cuenta que este modelo tiene una base matemática muy fuerte. Esto no debe asustarnos, en principio, ya que es lo que le proporciona su potencia y seguridad. Es cierto que también complica su estudio, pero afortunadamente, no tendremos que comprender a fondo la teoría para poder manejar el modelo.

En el modelo relacionar define ciertos operadores. Estos operadores relacionales trabajan con tablas, del mismo modo que los operadores matemáticos trabajan con números. Esto implica que el resultado de las operaciones con relaciones son relaciones, lo cual significa que, como veremos, que no necesitaremos implementar bucles.

El álgebra relacional define el modo en que se aplican los operadores relacionales sobre las relaciones y los resultados que se obtienen. Del mismo modo que al aplicar operadores enteros sobre números enteros sólo da como salida números enteros, en álgebra relacional los resultados de aplicar operadores son relaciones.

Disponemos de varios operadores, que vamos a ver a continuación.

Selección

Se trata de un operador unitario, es decir, se aplica a una relación y como resultado se obtiene otra relación.

Consiste en seleccionar ciertas tuplas de una relación. Generalmente la selección se limita a las tuplas que cumplan determinadas condiciones.

<relación>[<atributo>='<valor>']

Por ejemplo, tengamos la siguiente relación:

tabla(id, nombre, apellido, fecha, estado)

tabla
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
102  Tulana   Liopez      24/6/1985   casado
554  Filgana  Gaomez      15/5/1998   soltero
005  Tutulano Gionzialez  2/6/1970    viudo

Algunos ejemplos de selección serían:

tabla[id<'200']
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
102  Tulana   Liopez      24/6/1985   casado
005  Tutulano Gionzialez  2/6/1970    viudo

tabla[estado='soltero']
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
554  Filgana  Gaomez      15/5/1998   soltero

Proyección

También es un operador unitario.

Consiste en seleccionar ciertos atributos de una relación.

Esto puede provocar un conflicto. Como la relación resultante puede no incluir ciertos atributos que forman parte de la clave principal, existe la posibilidad de que haya tuplas duplicadas. En ese caso, tales tuplas se eliminan de la relación de salida.

<relación>[<lista de atributos>]

Por ejemplo, tengamos la siguiente relación:

tabla(id, nombre, apellido, fecha, estado)

tabla
id   nombre   apellido    fecha       estado
123  Fulano   Prierez     4/12/1987   soltero
454  Mengano  Sianchiez   15/1/1990   soltero
102  Tulana   Liopez      24/6/1985   casado
554  Fulano   Gaomez      15/5/1998   soltero
005  Tutulano Gionzialez  2/6/1970    viudo

Algunos ejemplos de proyección serían:

tabla[id,apellido]
id   apellido
123  Prierez
454  Sianchiez
102  Liopez
554  Gaomez
005  Gionzialez

tabla[nombre, estado]
nombre   estado
Fulano   soltero
Mengano  soltero
Tulana   casado
Tutulano viudo

En esta última proyección se ha eliminado una tupla, ya que aparece repetida. Las tuplas 1ª y 4ª son idénticas, las dos personas de nombre 'Fulano' son solteras.

Producto cartesiano

Este es un operador binario, se aplica a dos relaciones y el resultado es otra relación.

El resultado es una relación que contendrá todas las combinaciones de las tuplas de los dos operandos.

Esto es: si partimos de dos relaciones, R y S, cuyos grados son n y m, y cuyas cardinalidades a y b, la relación producto tendrá todos los atributos presentes en ambas relaciones, por lo tanto, el grado será n+m. Además la cardinalidad será el producto de a y b.

Para ver un ejemplo usaremos dos tablas inventadas al efecto:

tabla1(id, nombre, apellido)
tabla2(id, número)

tabla1
id  nombre     apellido
15  Fulginio   Liepez
26  Cascanio   Suanchiez
 
tabla2
id   número
15   12345678
26   21222112
15   66525425

El resultado del producto cartesiano de tabla1 y tabla2: tabla1 x tabla2 es:

tabla1 x tabla2
id  nombre     apellido   id   número
15  Fulginio   Liepez     15   12345678
26  Cascanio   Suanchiez  15   12345678
15  Fulginio   Liepez     26   21222112
26  Cascanio   Suanchiez  26   21222112
15  Fulginio   Liepez     15   66525425
26  Cascanio   Suanchiez  15   66525425

Podemos ver que el grado resultante es 3+2=5, y la cardinalidad 2*3 = 6.