Conjunto de herramientas básicas para el control de la calidad,utilizado para la solución de problemas mediante el trabajo en equipo, y son: Histograma,diagrama de Pareto,diagrama Causa-Efecto( ó tambien conocido como diagrama de Ishikawa), hojas de Comprobación, gráficas de control, diagrama de Dispersión y Estratificación.
DIAGRAMA DE ISHIKAWA (CAUSA-EFECTO)
Objetivo:
Identificar las causas más probables de un problema (efecto).
Fue creado por Ishikawa en 1953, por lo que también es conocido por
ese nombre.
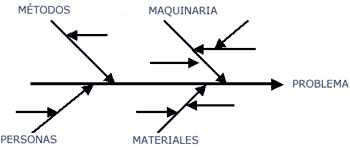
Consiste en una flecha horizontal en cuyo extremo derecho se sitúa la punta y se escribe el problema. A la flecha horizontal apuntan otras flechas que representan las causas principales (el número de éstas no debe exceder de 6) que pueden ser los cuatro componentes principales de cualquier actividad: métodos, maquinaria, personas y materiales. Hacia estas flechas de causas principales confluyen otras que representan causas secundarias que contribuyen a la existencia de las primeras.
Ventajas:
Método
racional para resolución de problemas.
Visualización de las causas de un problema.
Sistematización.
Fomento del trabajo en equipo.
Proceso:
- Definir el problema
- Determinar los factores o causas principales. Es aconsejable utilizar las categorías antes referidas (métodos, maquinaria, personas y materiales).
- Establecer, por medio de brainstorming o tormenta de ideas, las causas secundarias y de tercer nivel, si las hubiera.
- Una vez realizado el gráfico, reflexionar sobre la importancia y coherencia de las causas resultantes, aportando los argumentos pertinentes para obtener conclusiones.
Ejemplo del Diagrama Causa-Efecto
En un restaurante de menús diarios han observado que sus clientes se
quejan porque tardan demasiado tiempo en servirles. Para analizar las causas
de la tardanza, realizan entre todos los empleados el siguiente diagrama de
causa y efecto:
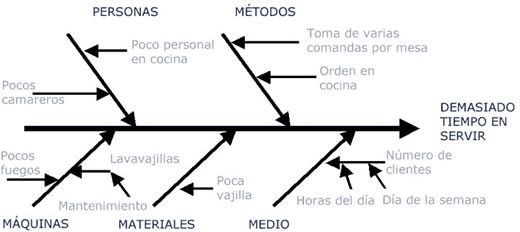
A la vista del diagrama y tras discutir y argumentar la importancia de cada causa, las prioridades de mejora y las posibilidades de actuación, la dirección del restaurante decide:
Invertir
en el mantenimiento y puesta a punto del lavavajillas para optimizar
el material existente.
Revisar más detenidamente los métodos para diseñar procesos
que agilicen el servicio en vez de retrasarlo, porque debido al reducido espacio
de la cocina (y a la imposibilidad de ampliarla por diversas razones), no es
factible instalar más la maquinaria.
Organizar los turnos laborales para potenciar los días de la semana
y las horas del día con más afluencia de clientes.
A la vista del diagrama y tras discutir y argumentar la importancia de cada
causa, las prioridades de mejora y las posibilidades de actuación, la
dirección del restaurante decide:
- Invertir en el mantenimiento y puesta a punto del lavavajillas para optimizar el material existente.
- Revisar más detenidamente los métodos para diseñar procesos que agilicen el servicio en vez de retrasarlo, porque debido al reducido espacio de la cocina (y a la imposibilidad de ampliarla por diversas razones), no es factible instalar más la maquinaria.
- Organizar los turnos laborales para potenciar los días de la semana y las horas del día con más afluencia de clientes.
Objetivo:
Detectar las principales causas de un problema para establecer prioridades
de actuación.
Basado en la ley de Pareto (Ley de la Prioridad) que establece que el 20% de
las causas producen el 80% de los efectos.
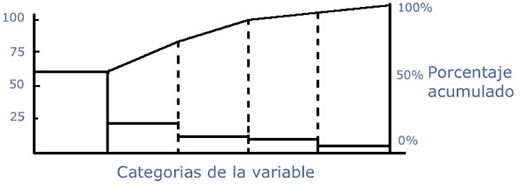
Se compone de un gráfico de barras que representa las frecuencias de la variable (categorías) ordenadas de mayor a menor, y una gráfica lineal superpuesta que indica el porcentaje acumulado de cada variable sobre el total.
Procedimiento:
- Determinar el problema y los datos que es necesario recoger.
- Construir una tabla de recuento de datos para constatar la frecuencia de cada categoría.
- Calcular las frecuencias relativas y acumuladas.
- Construir
el diagrama:
* El eje horizontal se divide entre las categorías medidas (causas o factores) del problema.
* El eje vertical izquierdo se numera desde 0 hasta el número total de frecuencias absolutas.
* El eje vertical derecho se numera con los porcentajes de 0 a 100.
* Los valores absolutos de cada factor se representan con barras, ordenadas de mayor a menor.
* Sobre el diagrama de barras se dibuja la gráfica de porcentajes acumulados.
Ejemplo
de Diagrama de Pareto
Una fábrica de automóviles tiene que mejorar uno de sus modelos
porque ha detectado que los costes de garantía son demasiado elevados.
Para ello se recogen datos sobre las averías durante el periodo de garantía de los automóviles vendidos en el último año.
Con estos datos se elabora el diagrama de Pareto siguiente:
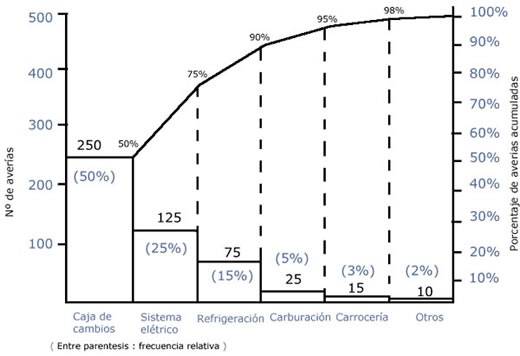
Siguiendo la Ley de la Prioridad, se debería actuar contra las causas de avería en la caja de cambios y en el sistema eléctrico, pues entre ellas suman aproximadamente el 80% de los efectos. (Primero se actuaría sobre las causas de avería en la primera, pues si se fabricaran cajas de cambio perfectas se reducirían las averías totales a la mitad).
Objetivo:
Recolectar datos de forma fácil y organizada.
También llamada de medidas, de verificación y de control.
Herramienta sencilla que permite que la información sea recogida por varias personas.
Sirve para cuantificar problemas, defectos, causas, cumplimiento de actividades, etc. Datos que más tarde se pueden usar para realizar gráficos y análisis diversos.
Con esta técnica se normaliza la captura de información para cada caso concreto. Cada usuario debe diseñar la hoja de registro según su problemática particular.
Proceso:
Seleccionar
el tipo y la cantidad de información a recoger.
Determinar el tiempo de recogida de datos.
Diseñar el impreso de hoja de registro.
Procesar y analizar la información.
Utilizar, si procede, en la elaboración de gráficos o en otras
técnicas.
Ejemplo:
Una fábrica de automóviles necesita recoger datos sobre las averías de uno de sus modelos durante el periodo de garantía. Para ello diseña una hoja de registro que envía a los talleres concertados:
Caja de Cambios IIII IIII IIII III 33 Sistema Eléctrico IIII II 7 Refrigeración HH IIII 9 Carburación III 3 IIII II 7
DIAGRAMA
DE DISPERSIÓN
Objetivo: Determinar si existe relación entre dos variables.
Sirve para poner de manifiesto si el comportamiento de una variable influye
en el comportamiento de otras, es decir, si la variación de una característica
puede ser causa del efecto en otra. Es pues una técnica que ayuda en
el control de procesos.
Consiste en la representación gráfica, en un eje de coordenadas, de los pares de valores correspondientes a las variables estudiadas por medio de puntos.
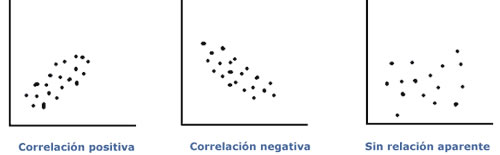
Según el aspecto de la nube de puntos en el gráfico, se pueden establecer tres tipos de relación:
Correlación
positiva: indica que al aumentar una de las variables aumenta
la otra
Correlación negativa: indica que
al aumentar una de las variables disminuye la otra.
Sin relación aparente.
Procedimiento:
- Recopilar los pares de datos de una muestra de al menos 30 datos.
- Determinar la escala del dibujo para que la amplitud de los ejes sea aproximadamente la misma.
- Colocar
los puntos en el gráfico. Cada punto corresponde a un par
de datos (x,y). Si hay más de un punto con las mismas coordenadas
se rodea con un círculo.
Ejemplo de Diagrama De Dispersión
Una empresa quiere determinar si la dedicación de parte del horario laboral de sus empleados a la formación perjudica la producción.
Se recogen datos de los índices de producción y las horas dedicadas a formación cada semana durante siete meses. Se realiza una muestra por cada trabajador para no incurrir en errores por el uso de datos de estratos distintos (lo que, además, proporciona un control individual de rendimiento). Y se realizan, con los datos recogidos, diagramas de dispersión.
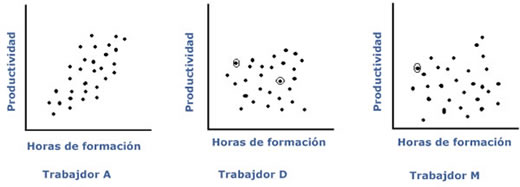
De la observación de los gráficos resultantes se extraen las siguientes conclusiones:
En
la mayoría de los casos no se observa correlación alguna.
En aquellos casos en que sí hay correlación, ésta es positiva,
o sea que el aumento de horas de formación conlleva un aumento en la
producción.
Sería conveniente estudiar los casos de correlación positiva
para determinar si se debe a que los contenidos de formación se corresponden
con las tareas a realizar, y si es así, ajustar en esta línea
la formación en los casos en que no hay correlación.
Como conclusión final: la formación en horario laboral no perjudica
la producción.
HISTOGRAMA
Objetivo: Representar gráficamente la distribución de frecuencias
de una determinada variable.
Consiste en un gráfico de barras que representa en el eje de abscisas
la variable segmentada en intervalos o clases (cada una de las barras), y en
el eje de ordenadas, la frecuencia de ocurrencia.
Sirve
para agrupar gráficamente un gran número de datos (se
recomienda hacerlo a partir de 50 datos como mínimo), y para
observar la pauta de variación de un proceso.
Procedimiento:
Reunir
los datos de la variable a estudiar (como mínimo 50).
Calcular el rango (R) o diferencia entre los datos menor y mayor.
Establecer el número de intervalos o clases (C) de la variable (barras
del histograma). Para ello se recomienda la raíz cuadrada del número
total de datos (D) (C= D ).
Calcular la amplitud (A) de cada clase dividiendo el rango (R) entre el número
de clases. (A=R/C).
Calcular los límites de cada clase. Tomando el valor más pequeño
y sumándole la amplitud de clase se obtiene el límite inferior
de la clase o intervalo siguiente, y así sucesivamente.
Contar el número de ocurrencias de cada clase.
Representar el histograma: En el eje de abscisas las clases nominadas con el
intervalo de datos que la limitan, y en el de ordenadas, sus frecuencias.
Nota: En la práctica los cálculos deberán ser, en la mayoría
de los casos, aproximados o redondeados.
EJEMPLO DE HISTOGRAMA
Una empresa ha implantado en su organización un sistema de gestión de reclamaciones. Para realizar un seguimiento del mismo, entre otras técnicas, se utiliza un histograma del tiempo de contestación al cliente:
Recogida
de datos de 81 reclamaciones contestadas (D=81).
Cálculo del rango: Dato mayor: 34 días. Dato menor: 7 días.
R=34-7=27
Número de intervalos o clases (número de barras del gráfico):
81 = 9 clases.
Amplitud de clase (el rango partido por el número de clases, A=R/C):
A=27/9 = 3.
Límites de clase: Sumando el valor más pequeño y la amplitud
(7+3) se obtiene el límite inferior de la siguiente clase (10), y así sucesivamente:
7 a 9 días, 10 a 12 días, 13 a 15 días...Una de las clases
debe contener cuatro valores. En este caso conviene que sea la clase última,
de 31 a 34 días.
Anotación del número de contestaciones comprendidas en cada clase
(frecuencia):
7 a 9 días : 4 contestaciones
10
a 12 " : 8 "
13 a 15 " : 10 "
16 a 18 " : 14 "
19 a 21 " : 20 "
22 a 24 " : 16 "
25 a 27 " : 4 "
28 a 30 " : 3 "
31 a 34 " : 2 "
Conclusiones:
Al implantar el sistema de gestión de reclamaciones, la empresa se propuso
contestar a los clientes en un plazo comprendido entre una semana y un mes.
A la vista del Histograma, los objetivos de la empresa tienen un alto grado
de cumplimiento. Aun así, la empresa inicia un proceso de mejora para
eliminar las contestaciones (2 en este estudio) fuera del plazo propuesto.
GRÁFICO
DE CONTROL
Técnica del control estadísticos de procesos (SPC) mediante la
cual se puede observar, analizar y controlar una determinada característica
de calidad.
Permite observar la evolución en el tiempo del proceso estudiado, evidenciando
los valores de la variable que están fuera de los límites de
control.
A partir de aquí se investigarán las causas de la situación fuera de control para reconducir el proceso dentro de los límites establecidos.
Consiste en un diagrama de líneas en el que se representan, calculados en base a los datos, unos límites de control superior (LSC) e inferior (LCI) entre los que deben estar la mayor parte de los valores de la variable, representada por una gráfica lineal:
Técnica utilizada en combinación con otras herramientas de análisis
de datos.
Sirve para separar los datos procedentes de distintas fuentes.
Se usa en combinación con histogramas, diagramas de dispersión, hojas de registro, etc., cuando los datos tienen diversas procedencias, por ejemplo: turnos de trabajo, trabajadores, días de la semana, suministradores, etc.