5.5 Tercera Forma Normal.

Para definir formalmente la 3FN necesitamos definir dependencia transitiva: En una afinidad (tabla bidimensional) que tiene por lo menos 3 atributos (A,B,C) en donde A determina a B, B determina a C pero no determina a A.

Definición formal:

Una relación R está en 3FN si y solo si esta en 2FN y todos sus atributos no primos dependen no transitivamente de la llave primaria.

Consiste en eliminar la dependencia transitiva que queda en una segunda forma normal, en pocas palabras una relación esta en tercera forma normal si está en segunda forma normal y no existen dependencias transitivas entre los atributos, nos referimos a dependencias transitivas cuando existe más de una forma de llegar a referencias a un atributo de una relación.

Por ejemplo, consideremos el siguiente caso:

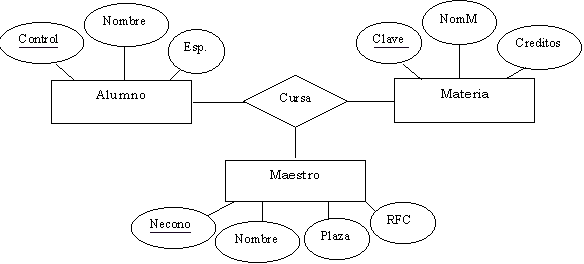
Tenemos la relación alumno-cursa-materia manejada anteriormente, pero ahora consideramos al elemento maestro, gráficamente lo podemos representar de la siguiente manera:

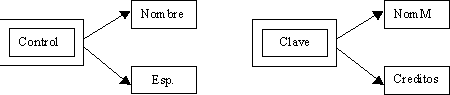
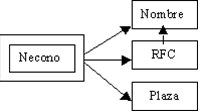
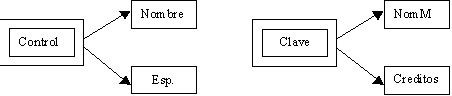
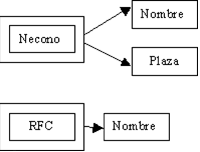
Podemos darnos cuenta que se encuentra graficado en segunda forma normal, es decir que todos los atributos llave están indicados en doble cuadro indicando los atributos que dependen de dichas llaves, sin embargo en la llave Necono tiene como dependientes a 3 atributos en el cual el nombre puede ser referenciado por dos atributos: Necono y RFC (Existe dependencia transitiva), podemos solucionar esto aplicando la tercera forma normal que consiste en eliminar estas dependencias separando los atributos, entonces tenemos:

Para definir formalmente la 3FN necesitamos definir dependencia transitiva: En una afinidad (tabla bidimensional) que tiene por lo menos 3 atributos (A,B,C) en donde A determina a B, B determina a C pero no determina a A.
Una tabla está normalizada en esta forma si todas las columnas que no son llave son funcionalmente dependientes por completo de la llave primaria y no hay dependencias transitivas. Comentamos anteriormente que una dependencia transitiva es aquella en la cual existen columnas que no son llave que dependen de otras columnas que tampoco son llave.

Cuando las tablas están en la Tercera Forma Normal se previenen errores de lógica cuando se insertan o borran registros. Cada columna en una tabla está identificada de manera única por la llave primaria, y no deben haber datos repetidos. Esto provee un esquema limpio y elegante, que es fácil de trabajar y expandir.